要約: Neural Style Transfer via Meta Networks

http://openaccess.thecvf.com/content_cvpr_2018/papers/Shen_Neural_Style_Transfer_CVPR_2018_paper.pdf

Style Transferに取り組んだ研究

Style転移の元とする画像を入力として、Style転移用のNeural Networkの重みを出力させるようなNeural Networkを学習させて用いるといった枠組みを提案

この論文で目指すこと

Style Transferのための手法としてはGatysらのもの(CVPR2016, https://www.cv-foundation.org/openaccess/content_cvpr_2016/papers/Gatys_Image_Style_Transfer_CVPR_2016_paper.pdf)が有名である。これはConvolutional Neural Networkの中間層における1次、2次統計量がStyle画像とContent画像で一致するようにContent画像を誤差逆伝播でIterativeに更新していく手法である。 この手法はそれらしい結果が得られる一方で、画像を誤差逆伝播でIterativeに更新していくためStyle Transferに時間がかかるという問題点がある。

一方でJohnsonらの手法(ECCV2016, https://arxiv.org/abs/1603.08155)は、Style画像ごとにStyle転移用のNeural Networkを学習させることで新規のContent画像に対して高速にStyleを転移させることを可能としているが、Style画像ごとにモデルを学習させる必要があり新規のStyle画像に対して対応するのが手間である。

そこでこの論文では新規のStyle画像、Content画像のペアに対してReal-timeにStyle Transferを行う手法の構築を目指す。

• なお、これを実現している手法としてすでにHuangらの手法(ICCV2017, https://arxiv.org/abs/1703.06868)があるものの、提案手法とはアプローチが異なる

手法

Style Transferで最も重要なのはStyle画像のStyleをContent画像に写す関数をどう定義するかである。 この論文ではStyle変換器としてNeural Networkを用いるが、そのNetworkのパラメータを用意するためにStyle画像を入力としてStyle変換器のパラメータを直接出力するようなモデルを学習させて用いる。

具体的なアルゴリズムは以下の通り。Style画像をMeta Networkに出力してパラメータwを計算して、そのwによって定義されるStyle変換器N(・; w)を用いて画像を変換し、変換後の画像について損失関数を計算してモデル学習に使う。

実験結果

ある程度それらしい結果が得られている。

感想

Style Transferのための枠組みとしてはICCV2017のHuangらの手法の方がよりフレキシブルに使えて良いのではないかとは思う。

しかしながら、Neural Networkの重みを吐き出させるNeural Networkを学習させるような枠組みが(少なくともこのタスクでは)上手くいくということを示しているという点でこの論文は極めて衝撃的である。

要約: The Mechanics of n-Player Differentiable Games

http://proceedings.mlr.press/v80/balduzzi18a/balduzzi18a.pdf

ICML2018の準Best Paperの論文

n人のプレイヤーがそれぞれのモデルパラメータをそれぞれについて設定された目的関数について学習していく際のパラメータの挙動について論じている

また、Nash均衡に行き着くための新たな学習アルゴリズムを提案し、それを2-player gameの一種であるGANの学習に応用している

この論文の面白いところ

非強調ゲームにはPotential gameというものとHamiltonian gameというもの(および両方の側面を併せ持つもの)がある。

特に、じゃんけんの三すくみやポケモンのタイプ相性のように"相性"があるゲームはHamiltonian gameになっていることが多い。

Potential gameは勾配降下法で簡単に最適化(=局所Nash均衡になる点を求めること)ができる一方、Hamiltonian gameでは勾配降下法を使っても最適化がうまく行かないという問題が知られていた。

じゃんけんを例に出すと、最適化の初期値としてプレイヤー1もプレイヤー2もチョキを100%出すという戦略から始める時、最適化のステップ1の後では学習の結果二人ともグーを100%出すという戦略になり、ステップ2の後ではパーを100%出すと言う戦略になり、...と言う感じでぐるぐると解の空間の中を回ってしまうという問題が知られていた。

この論文では、実際の目的関数に勾配ベクトルの長さを加えることでHamiltonian gameであってもうまく最適化できるようにする手法を提案している。頭よすぎ。

問題設定

Gameは、次の二つによって定義されるとする。

(1)n人のプレイヤー。

(2)n人のプレイヤーそれぞれについて設定された二回微分可能な損失関数。

それぞれのプレイヤーはモデルパラメータの調整を行なって、それぞれに対して設定された損失関数をなるべく小さくすることを目指す。

• これになぞらえると、GAN学習問題は「プレイヤーが二人いて、一方が識別器のパラメータを調整して識別器の損失を、もう一方が生成器のパラメータを調整することで識別器の損失に負の定数をかけたものを小さくすることを目指す」ゲームであると説明できる。

なおこの論文ではそれぞれのプレイヤーの損失関数をそれぞれのプレイヤーが制御できるパラメータで微分したものを次の記号で表現する:

ここで、はi番目のプレイヤーに対して設定された損失関数、はi番目のプレイヤーが制御できるモデルパラメータである。

また、以降ではi番目のプレイヤー以外のパラメータはまとめてと表記する。

局所Nash均衡

パラメータの近傍をと定義する。 局所Nash均衡とはN個のパラメータが全て次の条件を満たす場合のことである:

[tex: l_i(\hat{w_i}, w{-i}) \geq l_i(w_i, w{-i}) for \hat{w_i} \in U_i ]

Potential GameとHamiltonian Game

GameのHessianを次のように定義する (通常のHessianとは微妙に異なるので注意):

もしくは

Hessianは通常の行列と同様に次のように対称行列S (S=S^T)と交代行列A (A=-A^T)の和に分解できる:

Aが零行列のときは特にPotential Gameと呼ばれるものであり、過去によく研究されてきた。 一方でSが零行列のときはあまり研究がされてこなかった。この論文ではSが零行列のときをHamiltonian Gameと呼ぶこととしている。

Potential Game

Potential Gameとは任意のtex: w_i, w'i, w''iに対して次の条件を満たすような関数φとN個の正の数 (この論文の中ではと考えて良い)が存在するGameのことである:

これは次と等価であることが示されている:

(こちらのPDFもPotential gameについて解説しており、よりわかりやすい) https://www.jstage.jst.go.jp/article/sicejl/55/11/55_996/_pdf

Potential Gameの例としては、N人のプレイヤーが同じモデルのパラメータを同じ目的関数についてそれぞれ独立して最適化する場合などが挙げられる(N人が別々に識別器を学習させる場合など)。

Potential Gameではξを用いた勾配降下法によってφの局所最適解にたどり着けることが容易に示せる。

Hamiltonian Game

Hamiltonian Gameの例としては以下のものが挙げられる。

Hamiltonian GameはPotential Gameとはかなり性質の異なる概念である。 Potential Gameの場合と同様にプレイヤーにξを用いた勾配降下法によってパラメータを最適化させたいところだが、そうすると以下の図の左ようにくるくる回ってしまう場合もあり、局所Nash均衡に行き着くと限らない。

次の定理では次に定義するHamiltonian H(w) (HessianのHと紛らわしいが異なるので注意) について勾配降下法を適用することで局所Nash均衡にいきつけるということを示唆している。

上の図の右側に示されるようにH(w)についての勾配を用いることで局所Nash均衡に向かって正しくパラメータ更新ができるようになる。

一般的な場合において局所Nash均衡を得るためのアルゴリズム

ここまでで、Potential Gameではξを用いた勾配降下法によって、Hamiltonian GameではHamiltonian H(w)について勾配降下法を適用することによってそれぞれ局所Nash均衡に辿りつけることがわかった。

次にPotential GameでもHamiltonian Gameでもない一般的なGameにおいて局所Nash均衡にたどりつけるようなアルゴリズムを検討していく。 具体的には、勾配ξを少し修正して用いることで安定した固定点にパラメータが向かっていくように仕向けることを考える。

• 勾配ξを修正する手法としてConsensus Optimizationというものがすでに提案されているが、これは安定した固定点に行き着く保証がない。

この論文では、次に示す方法で勾配ξを修正することを提案している:

これをSymplectic Gradient Adjustment (SGA)と命名している。 Smyplecticという単語はSymplectic geometryという概念に起因している

この更新式は、次の三つの望ましい条件を満たしているところが理想的である: 

 

(ただしD3はλが正であるときに成り立つ)

なお、上記のアルゴリズムはλの選び方に余地がある。仮にλの符号を次の条件が満たされるように選んだとする:

この時、更に望ましい2つの条件が満たされるような更新式になる:

最終的なアルゴリズムは以下の通りである:

合成データでのSGAとGradient Descentの比較

以下の損失関数を元にした2プレイヤーゲームを考える。プレイヤー1はxを調整してを、プレイヤー2はyを調整してを下げることを目指す:

この時にGradient Descentを使った場合(ξをそのままパラメータ更新に使った場合)とSGAを使った場合を比較した図が以下の通りである:

GAN学習の実験

16種のGaussianからなるGMMをGANで近似する実験を行なっている。以下の図がその結果である:

通常のGradient DescentだとMode Collapseが発生しているが、提案法だと16種のMode全てをある程度捉えることに成功している。

要約: Multiclass Spectral Clustering

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.449.5354&rep=rep1&type=pdf

なるべく良いSpectral Clusteringの離散解を得るためのアルゴリズムを提案した論文

前置き: Multi-class Spectral Clustering 

Multi-class Spectral Clusteringの目的関数:

なお、Wは類似度行列、Dは以下に示す通りの次数の行列である:

この問題(Eq. 11~13)はNP困難であるため、Xを連続値に緩和して解くことを考える。 ここで、Zを以下のように定義する:

このZと連続値緩和により、問題Eq. 11~13は次のように書き換えられる:

この問題の解集合は次のように書き下せることが簡単な計算で示せる:

ここで、Pは以下の行列である:

また、Λ*はPの固有値を対角成分に並べた行列である。

この結果得られたZの解集合をXに戻すことで、当初の問題(Eq. 11~13)でXを連続値緩和した場合のXの解集合が得られる。 ここで、XからZへの変換をZ=f(X)とすると、f(X)には次のような逆変換が存在するということに注目したい:

さらに、f(X)の逆変換について次が成り立つことに注目したい:

Eq.24とEq.30から、問題Eq. 15~16に対応するXの解集合は次のように表せる:

連続値緩和した解の離散化

当初の問題(Eq. 11~13)を連続値緩和した問題(Eq. 15~16)のXの解集合は上記の手順で求められることはわかった。 この論文ではその解集合を用いて、当初の目的関数Eq. 11をなるべく大きくするような離散解(というかクラスタリング結果)を効率的に求める方法を提案している。

具体的には、Eq. 30の解集合に含まれるいずれかの連続解までの距離が最も小さくなる離散解Xを求めて出力することを提案している:

問題Eq. 31~33を解くために、この論文ではXとRの交互最大化に基づくアルゴリズムを提案している。

Rを固定したときはEq. 31のφ(X, R)を最大化させるXは次のように効率的に求められる:

逆にXを固定したときはEq. 31のφ(X, R)を最大化させるRは次のように効率的に求められる:

ここで、Eq. 40の右側は左側の特異値分解である。

この論文のSpectral Clusteringのアルゴリズムをまとめると、一旦連続値緩和した場合の解を得た上で、それをもとにEq. 36とEq. 39を交互に解くことで離散解Xを求めるというアルゴリズムである。

k-meansほど初期値依存性などがなくて良いとのこと。

余談

scikit-learnのSpectral Clusteringでassign_labelsという引数に”discretize”という文字列を渡すことでこのアルゴリズムを利用できる。

要約: NAM: Non-Adversarial Unsupervised Domain Mapping

新たなDomain変換の手法Non-Adversarial domain Mapping(NAM)を提案。GANに基づかないので安定して射影の学習が可能。

Non-Adversarial Exact Matching

単純な仮定が成り立つ場合から始める。ドメインXとYから得られたデータ集合{}と{}を考え、それぞれのに対応するデータが{}の中に含まれていてそれがを満たすと仮定する。そのようなxとyのペアを探したい場合、(1)xとyのマッチングを推定する、(2)変換T(・)を推定する、という二つの問題を解くことになる。これを式に起こすと次のようになる:

ここでMijはマッチすると推定されたときには1、そうでないときには0になる変数であるとする。 これを最小化するのは困難である。そこで、Mについてのバイナリの制約条件を[tex: M{ij} \geq 0]、[tex: \sum_j M{ij} =1]という制約に緩和して最小化するような枠組みが提案されている。これはANGAN (Identifying analogies across domains, ICLR2018)と呼ばれる手法である。

Non-Adversarial Inexact Matching

実際にはドメインXとYの間でのExactなマッチングは存在しない(つまり1対1対応していない)ことが多い。そのような場合には、それぞれのyについてy=T(x)を満たすようなxがドメインXのデータ集合{}の中に存在するという仮定自体を見直すべきである。

そこでこの論文では、yに対応するxをドメインXのデータ集合{}の中から探してくるのではなく、ドメインXに属していてかつを満たすようなをそれぞれのyごとに擬似的に生成するという枠組みを提唱している。

擬似的に生成する方法としては様々なものが考えられるが、例えば次のようにを定義するという方法が挙げられる:

しかしながらこの方法には、ドメインXに含まれるデータのsimplexでは適切なデータを生成することができないという問題点や、パラメータ数がデータ数の二乗のペースで増加していくという問題点がある。

Non-Adversarial Mapping (NAM)

この論文ではなんらかの手法(GANやVAEなど)を用いて既に手元に潜在変数からのドメインXのデータの生成器G(・)があるとして、それを用いてyに対応するドメインXのデータxを生成することを考える。 具体的には、次の目的関数を最小化することによりそれぞれのyに対応するxを生成する潜在変数zと射影T(・)を同時に学習する。この研究ではこれをNon-Adversarial Mapping (NAM)と命名している:

(3)の損失としてはSemanticなラベルで学習済みのCNNを用いたPerceptual Lossを使用することを提唱している:

NAMはGANベースの手法とは異なり安定して学習ができるという利点を有する。

なお、xに対応するyではなくyに対応するxを求めたい場合には(3)の潜在変数だけを更新するようにすれば良い。

実験結果の例

要約: GANimation: Anatomically-aware Facial Animation from a Single Image

http://openaccess.thecvf.com/content_ECCV_2018/papers/Albert_Pumarola_Anatomically_Coherent_Facial_ECCV_2018_paper.pdf

ECCV 2018 Best Paper Honorable Mention

表情編集のためのGANを提案した研究。心理学分野における"Facial Action Coding System"という枠組みと関連付けながら説明している。

Facial Action Coding System

心理学の分野では、EkmanとFriesenらにより"Facial Action Coding System"(FACS)と呼ばれる顔の表情を解釈する方法が提案されている。 FACSでは別々の表情筋に対応した"Action Unit"という概念を導入し、そのAction Unitの組み合わせによって表情が表現されるとしている。 人間は30種類のAction Unitしか発見されていないが、それらの動かし方の組み合わせで7000以上の表情を表現することができるとのことである。

提案法

大まかなフレームワークが以下の図。 入力画像の他にAction-Unitの状態を記述するための変数を用意し、これを同時に入力として与える。

Generator

Generatorは以下のように、画像とAction-Unitの状態を元にColor MapとAttention Mapを出し、Attention Mapで反応しているところだけ画像を修正する。

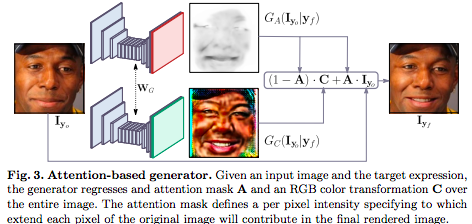
こうすると確かに画像のボヤケが生じうる範囲を小さくできるので良さそう。

Conditional Critic (Discriminator)

DiscriminatorとしてはPatchGANのようにPatchごとに評価を下すものを採用。また、Action-Unitの状態を推定するためにDiscriminatorの先頭(というか分枝)にを評価するための出力層も用意。

損失関数

4種類(が2項あるため計5項)の損失項の線形和によりモデルを学習させる。

Image Adversarial Loss ()

WGAN-GPで用いられる損失項。生成画像がデータセット内の画像と類似したものになるように働きかける。

Attention Loss ()

隣り合う画素のAttentionが近くなるように、かつAttentionがかかり過ぎないようにする損失項。

Conditional Expression Loss ()

Action-Unitの状態で条件づけられて生成された画像がちゃんとという状態に従うようにはたらきかける損失項。

IdentityLoss ()

CycleGANのように戻ってきた結果が同じ画像になるようにする損失項。要素ごとのL1距離で測る。

実験

Action Unitの可視化

それぞれのAction-Unitで違う表情が表現されていることがわかる。

感情編集

感情Aに対応するAction-Unitの状態を推定する方法が論文中に見当たらない。(感情Aに対応する顔画像の集合からAction-Unitの状態をDiscriminatorを用いて計算して平均を取るなどだろうか)

Image editing in the wild

一応顔検出器と適切に組み合わせることでいわゆる”wild”な画像の編集もそこそこできる:

彫刻・絵画の編集

彫刻・絵画の写真の編集もある程度できる。下側は失敗した例。サイクロプスのような画像の編集は難しいか。

感想

Maskを用いた顔編集によりぼやけの小さい画像編集ができることを提案したこと、及びAction-Unitという概念を元にした提案手法の解釈、そしていわゆる”wild”な画像や彫刻・絵画の画像の編集ができることを提示していることが貢献であると思われる。

Action-Unitという概念と絡めつつ説明しているものの、別にAction-Unit の各要素が別々の筋肉に対応しているとは言えず、言ったもん勝ちではという印象もある。 また、Maskを用いた顔編集を提案したことも評価されているところの一つであると思われるが、どこかで聞いたような気もするのでそんなにすごいのかとは思わなくもない。

要約: Implicit 3D Orientation Learning for 6D Object Detection from RGB Images

http://openaccess.thecvf.com/content_ECCV_2018/papers/Martin_Sundermeyer_Implicit_3D_Orientation_ECCV_2018_paper.pdf

ECCV18 Best Paper Award

高速に6DoF物体検出(位置だけでなく対象物体の姿勢情報も同時に推定する問題)を行う方法を提案。 検出対象とする物体のCADモデルさえあれば6DoFの情報を付与した学習用画像データがなくても6DoF物体検出モデルの学習ができるという点が強み。

パイプライン概要

高速な物体検出器であるSSDを用いて位置情報を先に推定し、その上で姿勢情報を推定するという流れ。

基本的にはRGB画像を入力として想定。とはいえDepth情報があればIterative Closest Pointアルゴリズムを利用してさらに結果を改良することもできる。

この論文のキモは後段の姿勢情報の推定法である。

姿勢情報の推定

RGB画像から物体の姿勢情報を推定するのがそこまで簡単でないのは、例えば(1)それぞれの画像で背景が異なっていたり、また(2)物体が部分的に隠れていたりすることなどが主な原因であると言える。 この論文では(1)(2)の影響を排除するためにDenoising AutoEncoder (AE)に基づいたAugmented AEという枠組みを提案し、Augmented AEを用いて姿勢推定を行う方法を提案している。

Denoising AEはノイズの加わったデータを入力として、そのデータからノイズを除去したデータを出力するようなAEである。 これをアナロジーにこの論文では、特定の背景を持っていたりオクルージョンのある物体の画像を入力として、その背景とオクルージョンを無くした画像を出力するようにAEを学習することを提案し、それをAugmented AEと命名している。

下の図が学習の概要。学習時には「背景及びオクルージョンのある物体の画像」と「物体だけが移る画像」のペアが必要だが、これはCADデータとランダムに集めた背景用画像を元に作成する。

テスト時の流れ

あらかじめ対象物体のあらゆる姿勢の画像をCADデータを元に生成しておき、Augmented AEのEncoderを用いてそれぞれの潜在表現を計算しておく。 テスト対象とする画像が入力されたら、SSDで物体検出し、検出された領域をAugmented AEのEncoderに入力して潜在表現を計算する。あとは計算済みのそれぞれの姿勢に対応する潜在表現の集合からその潜在表現と類似したものをCosine距離に基づいて検索し、結果を出力する。

感想

6DoF情報を付与した学習用データがなくても使えるのがよい。 逆にCADデータ(というか対象物体の3次元モデル)が必要であるというところは欠点であるとも言えるが、3次元復元技術と組み合わせればそんなに問題にはならないという気もする。 Augmented AEの入力データ作成の方法は例えば光源位置を変えたりするなどによりもう少し改良ができそう。

要約: Neural Optimizer Search with Reinforcement Learning

http://proceedings.mlr.press/v70/bello17a/bello17a.pdf

ICLR17のoral枠のNeural Architecture Search with Reinforcement Learningの手法を応用してOptimizer自体を最適化することを目指した研究

Optimizerの更新規則の表現方法

この論文では、Optimizerの更新規則自体を最適化することを目指す。
その上で、Optimizerの更新規則を以下の式を（場合によっては再帰的に）用いて表現することとする：

ここで、u_1とu_2は入力変数が1つの関数を、bは入力変数が2つの関数を、op_1とop_2は入力として何を使うかを表現している。
例えばSGDを表現したい場合、u_1とu_2にはidentity mapping（つまり入力をそのまま出力させるだけの関数）を、bには積を、op_1とop_2にはそれぞれ勾配と定数（例えば1など）を設定すれば良い。
RMSPropを表現したい場合、u_1にはidentity mappingを、u_2にはSquare rootを、bにはu_1(op_1) / u_2(op_2)を、op_1とop_2にはそれぞれ勾配と勾配の二乗の移動平均を設定すれば良い。
またADAMを表現したい場合、上記の式を1度使うだけでも表現できるし、以下のように再帰的に二度使うことによって表現することも可能である。

Controllerの定義

Controller(optimizerのデザインを出力するモデル)は、毎回の試行に際しOptimizerの更新規則を出力する。
この論文ではRNNを用いてControllerを構成する。RNNは毎回5n個（nは学習時には固定）の要素を出力し、その出力を元に更新規則を定義する。（以下の図を参照）

Neural Architecture Search with Reinforcement Learningで用いられている方法と感覚的には近い。

Controllerの学習方法

前段のNeural Architecture Search with Reinforcement LearningではREINFORCEを用いて学習を行なっていたが、この論文では学習が高速化されるということでTrust Region Policy Optimizationを使用したと述べられている。
学習はNeural Architecture Search with Reinforcement Learningで用いられた分散技術を利用して行う。

Optimizerの良さは、二層構造の単純なCNNを学習させて得られる精度を見て判断している。
というのも単純なモデルの学習がうまくできるOptimizerはより複雑なWide Residual Networkなどでもうまく動くだろうということでそうしたとのこと。 また学習は5 epoch回すだけにしたと述べられている。実験はCPU100個で1日以内に終了したとのこと。

実験

学習の設定

u_1、u_2、b、op_1、op_2として使ったものは以下の通り：

ここでm、v、γのhatはそれぞれg、g²、g³の移動平均。

実験はCifar10で行なって得られた結果のみが掲載されている。

結果

時間経過に伴ったReward Functionの推移。どんどんRewardが増えていっている。

最終的に得られたOptimizerの更新規則の中で、以下の二つが良さげだったとのこと：
、

これら二つの更新規則を用いて300 epoch分学習させた場合の精度曲線はそれぞれ以下の通り：

得られたOptimizerをより深いモデルへ応用

上記二つの更新規則を用いてWide ResNetを学習させた場合の精度曲線はそれぞれ以下の通り：

至極いい感じ。

GNMT（Google Neural Machine Translation）への応用

GNMTを学習させる際に、Neural Optimizer Searchで得られた良さげな更新規則の一つを用いた場合の結果：

ADAMより良さげ。
なおGNMTの学習は本来ADAM+SGDで行われているため、強いていうならそちらの値との比較もほしいところ。

その他感想

1. Neural Architecture Searchよりも実験が小規模であり、そこまで計算資源がないチームでも頑張れば再現実験ができそう。
2. Controllerの出力が可変長でないのであればBayesian Optimizationを使うだけで十分である気もする。